About Learning III

At the end of “training” (after model optimization), we need to ask the following:

  1. How well is our model doing?

  2. Is our model good enough for us to use?

To answer this, we must do model evaluation. And to evaluate, certain measurement or metric is used to judge (evaluate) the performance of your model. It provides a more interpretable measure of your model’s performance.

Also recall that our “learning” output answer will always be in terms of probability.

The end goal is to:

  • Optimal: our trained model(s) performs as well in unseen dataset
  • Reliable: our trained model(s) behaves as expected

Common metrics

Here are the essential metrics:

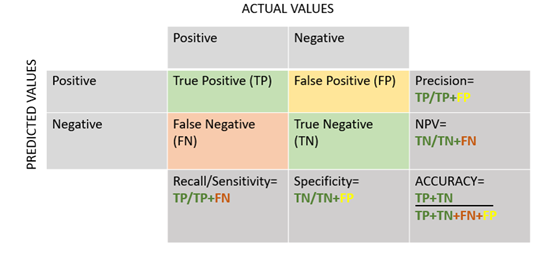
  • True Positives (TP) is an outcome where the model correctly predicts the positive class, and the actual value was also positive

  • True Negatives (TN) is an outcome where the model correctly predicts the negative class, and the actual value was also negative

  • False Positives (FP) is an outcome where the model predicted the positive class incorrectly, and the actual value was negative

  • False Negatives (FN) is an outcome where the model predicted the negative class incorrectly, and the actual value was positive .

Figure 1: common general metric

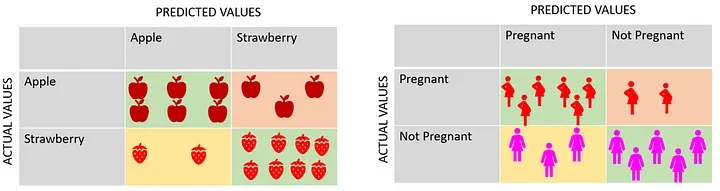
Example

Figure 2: Example 1
Figure 3: Example 2
Figure 4: Example 3

Precision (or correctness): This metric shows how often your model is correct when predicting the target class.

\[ Precision = \frac{TP}{TP + FP} \] Recall (sensitivity): a measure of how actual observations are predicted correctly.This shows whether your model can find all objects of the target class(how many correct items were found compared to how many were actually there)

\[ Recall = \frac{TP}{TP + FN} \]

  • High precision and high recall mean that your model is performing well.
  • Low precision means that your model will predict some false positives
  • Low recall means that your model will predict some false negatives

F1-score: is the harmonic mean of the precision and recall values

\[ F1 Score = \frac{2 \times Precision \times Recall}{Precision + Recall} \]