Introduction

First we must differentiate between data at hand - which is the data that is available to us, and data not in hand, which are data not yet available or will come in the future whereby the model will be applied on. True reliability of the model will be when tested against data not in hand. To understand this, we need to go back to data collecting.

Goodness of dataset

Before collecting data for your problem, we first need to know “what makes a good dataset”?

  • quality (representative and high-quality of inputs data)
  • quantity (consistent and accurate labels on target data/ground truth)
  • variability (reflect post deployment changes)

General Problem

Nowadays, the availability of large volumes of data and the widespread use of tools for the proper extraction of knowledge information has become very frequent.

Most learning systems usually assume (e.g. academic, kaggle data) that training datasets used for learning are balanced.

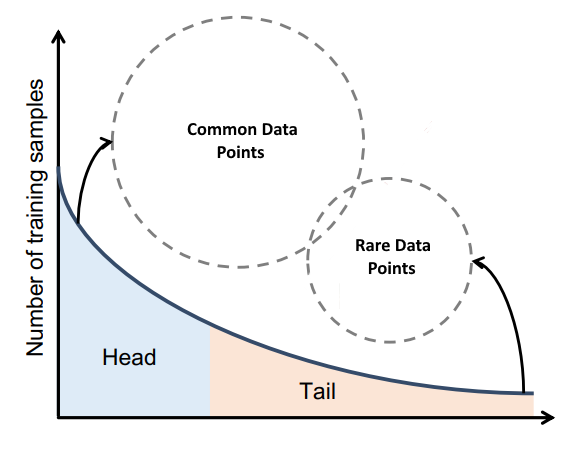
However, in real-world applications, training samples( data at hand ) typically exhibit a long-tailed class distribution, where a small portion of classes have a massive number of sample points but the others are associated with only a few samples1.

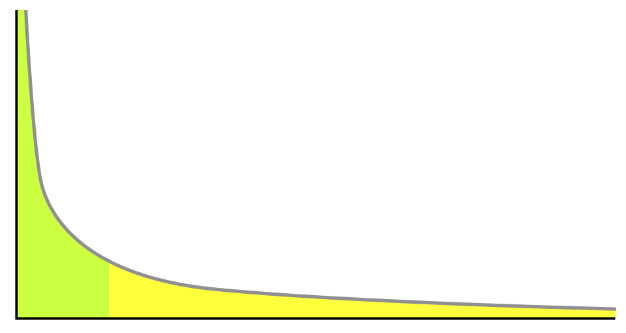
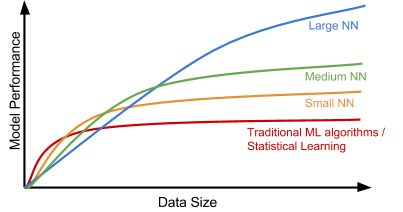
Figure 1: Long Tail Data Illustration

Long-tail data is visually represented by a hyperbolic curve like in Figure 1.

So long-tail data is the collection of all data about items that serve a specific niche and have a low demand but exist in greater varieties.

Consider example, in autonomous driving, you would want a model detecting pedestrians to work equally well, irrespective of the weather, visual conditions, how fast the pedestrian is moving, how occluded they are, et cetera. Most likely however, your model will perform much worse on cases that are more rare—for example, a baby stroller swiftly emerging from behind a parked car in unpleasant weather.

The point of failure here is that the model has been trained on data that was recorded during regular traffic conditions. As a result, the representation of these rare scenarios (as a portion of the entire training dataset) is much lower compared to common scenarios. Figure 2 is an example of two highway scenarios, whereas lane detection will be significantly more difficult in the right hand picture compared to the left.

Figure 2: long tail scenario

Thus, need to acquire more of these rare cases in our training data!

Figure 3: class imbalance problem

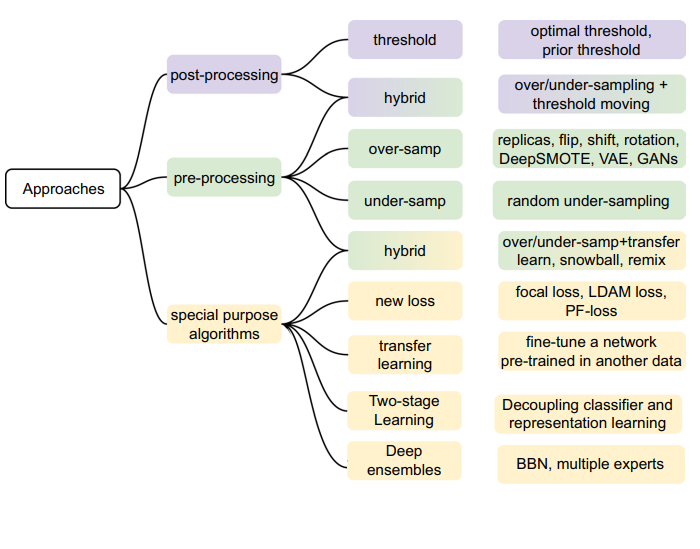
Addressing imbalanced dataset

  • Data sampling : in which the dataset instances are modified in such a way as to produce a more balanced class distribution.
  • Algorithmic modification
  • Cost-sensitive learning

Data sampling

Figure 4: Downsample and Upsample
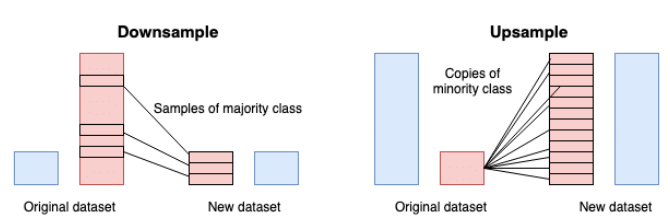
  • Upsampling : process of randomly duplicating observations from the minority class to reinforce its signal.
  • Downsampling: sample the majority class randomly to make their frequencies closer to the rarest class.
  • hybrid: some methodologies do a little of both and possibly impute synthetic data for the minority class.

Algorithmic modification

Instead of focusing on modifying the training set in order to combat class skew, this approach aims at modifying the classifier learning procedure itself.

Cost-sensitive learning

Cost-sensitive learning for imbalanced classification is focused on first assigning different costs to the types of misclassification errors that can be made, then using specialized methods to take those costs into account.

Figure 5: Three main categories of approaches proposed and tested for tackling the class imbalance problem. Main categories of approaches on the left, followed by subcategories and some examples on the right2

How much data?

Wisdom

“To answer the “how much data is enough” question, it’s absolutely true that no machine learning expert can predict how much data is needed. The only way to find out out is to set a hypothesis and to test it on a real case.” — Maksym Tatariants

“no learner(classifier) can beat random guessing over all possible functions to be learned” - no free lunch theorem3

The fundamental goal of machine learning is to generalize beyond the examples in the training set. This is because, no matter how much data we have, it is very unlikely that we will see those exact examples again at test time.

Question : To “learn” and achieve good generalization, how much data do we need?

Observed and test

  • increase the dataset sample size is a reduction in model over-fitting (avoid the model “memorize”)
  • be careful of noise, outliers, and irrelevant information in additional data (recall “Goodness of dataset”)
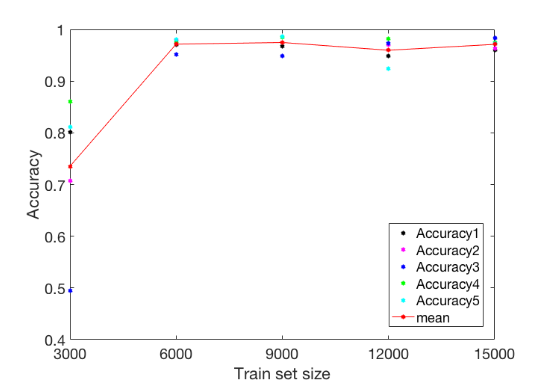
Figure 6: Model performance of deep learning vs. other machine learning algorithms as a function of number of samples.4

Observation 1:

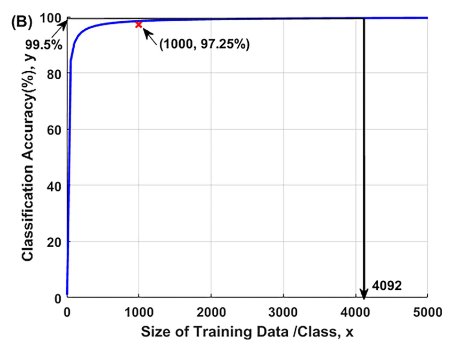
Figure 7: Effect of training data size on accuracy on cifar-10 images

Observation 2:

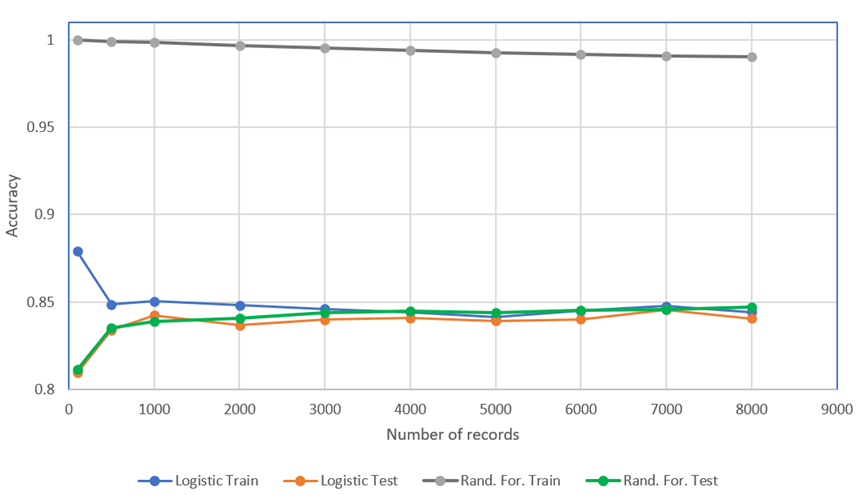
Figure 8: Effect of training data size on accuracy on medical(CT scan image) classification

Observation 3:

Figure 9: Effect of training data size on accuracy on credit card fraud detection

We always prefer large amount of data, but how large is large, and how big is big? This is a problem of sufficiency, because even though the data may be large, but contains insufficient entropy, will render the data to be small, despite the large size in bytes.

Wisdom

Entropy quantifies how much information there is in a random variable (recall variability)

References

1.
Zhang, Y., Kang, B., Hooi, B., Yan, S. & Feng, J. Deep long-tailed learning: A survey. (2023).
2.
Johnson, J. M. & Khoshgoftaar, T. M. Survey on deep learning with class imbalance. Journal of Big Data (2019) doi:10.1186/s40537-019-0192-5.
3.
Wolpert, D. H. The lack of a priori distinctions between learning algorithms. Neural Computation 8, 1341–1390 (1996).
4.
Ng, A. How scale is enabling deep learning. (2016).